Help is appreciated EditInt (((xy)/2)^2 (1(xy)/2)^2) dx dy, x=0 to 1, y=0 to 1 Extended Keyboard;Math(1 y^2) dx (1 x^2)d y = 0/math math\implies (1 x^2) dy = (1 y^2)dx/math math\implies \dfrac{dy}{1 y^2} = \dfrac{dx}{1 x^2}/math math

Slides Show
X 1 y 2 dx y 1 x 2 dy 0
X 1 y 2 dx y 1 x 2 dy 0- Hello, can anyone solve this equation?5 Problem 15 (xy2 bx2y)dx(xy)x2 dy = 0 First, for this to be exact M y = 2xy bx2 = 3x2 2xy = N x So b = 3 With this, find the solution to the DE f(x,y) = Z M dx = Z xy 23x2ydx = 1 2 x y2 x3y g(y) And solve for g(y) f y = x 2y x3 g0(y) = x3 x y So we didn't need g(y) This leaves 1 2 x 2y x3y = C 6 Problem 18 Done in




Obtain The General Solution X 2dx Y X 1 Dy 0 Chegg Com
But if I expand the bracket $(xy)^2$ before integrating I will get $$\varnothing_1=\int Mdx=\int (xy)^2dx=\int (x^22xyy^2)dx=\frac{x^3}{3}xy^2x^2y$$ Wich will lead to the solution $$\varnothing=\varnothing_1\varnothing_2=\frac{x^3}{3}xy^2x^2yy=Constant$$ What is the wrong step ?91 A product of several terms equals zero When a product of two or more terms equals zero, then at least one of the terms must be zero We shall now solve each term = 0 separately In other words, we are going to solve as many equations as there are terms in the product Any solution of term = 0 solves product = 0 as well Get an answer for 'solve the differential equation (2xy3y^2)dx(2xyx^2)dy=0 ' and find homework help for other Math questions at eNotes
Simple and best practice solution for (1y^2)dx(x^2yy)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Solve (1 xy)y dx x(1 – xy)dy = 0The substitution y = vx or x = vy transforms the equation {eq}M\left( {x,y} \right)dx N\left( {x,y} \right)dy = 0 {/eq} into a separable differential equation which can be solved easily Answer
X`sqrt(1y^2)dxysqrt(1x^2)dy=0` solve using variable separable 1 Educator answer Math Latest answer posted at AM Solve the IVP sqrt(1y^2)dxsqrt(1x^2)dy=0, y(0)=sqrt(3)/2 Answered by a verified Tutor We use cookies to give you the best possible experience on our website By continuing to use this site you consent to the use of cookies on your device as described in our cookie policy unless you have disabled them 1 1 y dy dx = x2 ∫ 1 1 y dy dx dx = ∫ x2 dx ∫ 1 1 y dy = ∫ x2 dx ln(1 y) = x3 3 C 1 y = ex3 3 C = ex3 3 eC = Cex3 3 y = Cex3 3 −1 Applying the IV 3 = Ce0 −1 = C −1 ⇒ C = 4 y = 4ex3 3 −1




Obtain The General Solution X 2dx Y X 1 Dy 0 Chegg Com




Solve The Following Differential Equations Y X Y 1 Y 1 2 Y X Y 1 X 2 L Y 2 X Y 2 0 Y
See the answer See the answer See the answer done loading Solve the differential eqn x^2(y1)dxy^2(x1)dy=0 Best Answer This is the best answer based on feedback and ratings 100% (1Y2 = x−lnx1c (110) ylnx dx dy = µ y 1 x ¶ 2, ylnxdx= (y 1)2 x2 dy, (y 1)2 y dy = x2 lnxdx, Z (y 1)2 y dy = Z x2 lnxdx, resolvemos la integral del lado izquierdo Z (y 1)2 y dy = Z y2 2y 1 y dy = Z µ y 2 1 y ¶ dy = y2 2 2y lny, resolvemos la integral del lado derecho Z x2 lnxdx= integral por partes, tomamos u =lnxdu= 1 xI can't figure it out, (1xy)^2 dx y^2 x^2 (1xy)^2 dy = 0 Thanks



Find The General Solution Of Y2dx X2 Xy Y2 Dy 0 Studyrankersonline




If Y Sqrt 1 X 1 X Prove That 1 X 2 D Y Dx Y 0 Askiitians
The general solution of the differential equation (1 y 2 )dx (1 x 2) dy = 0 is The general solution of the differential equation (1 y 2 )dx (1 x 2 ) dy = 0 is 1) x – y = C (1 – xy) 2) x – y = C (1 xy) 3) x y = C (1 – xy)(c) ( y 2 x y 1 ) dx ( x 2 x y 1 ) dy = 0With M = y 2 x y 1 and N = x 2 x y 1, note that ( N x M y) / ( x M y N ) = ( x y ) / ( x ( y 2 x y 1 ) y ( x 2 x y 1 ) ) = ( x y ) / ( x y) = 1 Thus, μ = exp ( ∫ d(xy) ) = e xy is an integrating factor The transformed equation is ( y 2 x y 1 ) e xy dx ( x 2 x y 1 ) e xy dy = 02xy9x^2(2yx^21)\frac{dy}{dx}=0, y(0)=3 en Related Symbolab blog posts Advanced Math Solutions – Ordinary Differential Equations Calculator, Linear ODE Ordinary differential equations can be a little tricky In a previous post, we talked about a brief overview of
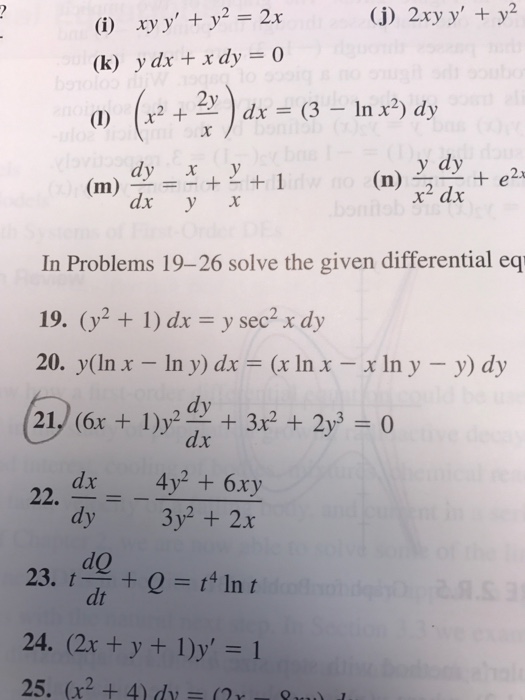



Xy Y Y 2 2x 2xy Y Y 2 Y Dx X Dy 0 X 2 Chegg Com



1
Find the particular solution of the differential equation x (1 y 2) dx – y (1 x 2) dy = 0, given that y = 1 when x = 0A first order Differential Equation is Homogeneous when it can be in this form dy dx = F ( y x ) We can solve it using Separation of Variables but first we create a new variable v = y x v = y x which is also y = vx And dy dx = d (vx) dx = v dx dx x dv dx (by the Product Rule) Which can be simplified to dy dx = v x dv dx Solve the differential equation x(y1) dx(x1)dy=0 If y=2 when x=1 Latest Problem Solving in Differential Equations More Questions in Differential Equations Online Questions and Answers in Differential Equations




Worked Example Identifying Separable Equations Video Khan Academy



How To Solve The Differential Equation Math X Sqrt 1 Y 2 Dx Y Sqrt 1 X 2 Dy 0 Math Quora
Since M yN x N =2 x, an integrating factor is μ (x) = 1 x 2, so the equation becomes exact (x 21 x y x 2) dx1 x dy = 0 Now, F = ∫ (x 21 x y x 2) dx = 1 3 x 3ln x y x g (y) and F y =1 x g ′ (y) =1 x = ⇒ g (y) = 0 Hence, 1 3 x 3ln x y x = c, or y = 1 3 x 4x ln x C 12 (2 xy 3 1) dx (3 x 2 y 2y1Click here👆to get an answer to your question ️ Solve the differential equation x(1 y^2)dx y(1 x^2)dy = 0Learn how to solve differential equations problems step by step online Solve the differential equation xy*dx(1x^2)dy=0 Grouping the terms of the differential equation Group the terms of the differential equation Move the terms of the y variable to the left side, and the terms of the x variable to the right side Simplify the expression \frac{1}{y}dy Integrate both sides of the




Solve X 2 D 2y Dx 2 X Dy Dx Y 0 Given That Y X 1 X Is A Solution Of It Youtube




Solution Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If
Ex 95, 4 show that the given differential equation is homogeneous and solve each of them (𝑥^2−𝑦^2 )𝑑𝑥2𝑥𝑦 𝑑𝑦=0 Step 1 Find 𝑑𝑦/𝑑𝑥 (𝑥^2−𝑦^2 )𝑑𝑥2𝑥𝑦 𝑑𝑦=0 2xy dy = − (𝑥^2−𝑦^2 ) dx 2xy dy = (𝑦^2−𝑥^2 ) dx 𝑑𝑦/𝑑𝑥 = (𝑦^2 − 𝑥^2)/2𝑥𝑦 Step 2 Putting F(x, y) = 𝑑𝑦/𝑑𝑥 and finding FClick here👆to get an answer to your question ️ Solution of (xy^2 x)dx (yx^2 y)dy = 0 By the way, the original equation 1x^2 dy/dx = 1y^2 is equivalent to x^2 dy/dx = y^2 with the solution ehild Unfortunately people on this board tend to be so sloppy with parentheses I just automatically assumed that was intended, but yes, the correct interpretation of what was written is as you say Share




The Solution Of Xsqrt 1 Y 2 Dx Ysqrt 1 X 2 Dy 0 Youtube



How To Get The Special Solution Of This Differential Equation Y Xdy Dx 2 1 X 2 Dy Dx Where X 1 Y 1 Quora
Calculus Find dy/dx y^2=1/ (1x^2) y2 = 1 1 − x2 y 2 = 1 1 x 2 Differentiate both sides of the equation d dx (y2) = d dx ( 1 1−x2) d d x ( y 2) = d d x ( 1 1 x 2) Differentiate the left side of the equation Tap for more stepsThe general solution of the differential equation 1 y 2 dx – 1 x 2 dy = 0 isx – y = C 1 – xyx – y = C 1 xyx y = C 1 – xyx y = C 1 xyQuestion Solve the differential eqn x^2(y1)dxy^2(x1)dy=0 This problem has been solved!



Solved Find The Particular Solution Indicated For The Following Course Hero



Find The General Solution Of The Differential Equation 1 Y2 X Etan 1y Dy Dx 0 Studyrankersonline
A solution of the differential equation (dy dx)2 − xdy dx y = 0 is 6 The differential equation corresponding to the equation y2 = a(b − x2) where a, b are constants is 7 If xy = Asinx osx is the solution of the differential equation xd2y dx2 − 5ady dx2xydxx2dy=0 Three solutions were found d = 0 y = 0 x = 0 Step by step solution Step 1 Equation at the end of step 1 3x2yd = 0 Step 2 Solving a Single Variable Equation What is the solution of the differential equation ydx (xx^2y)dy=0Watch Video in App This browser does not support the video element 1495 k 75 k Answer Step by step solution by experts to help you in doubt clearance & scoring excellent
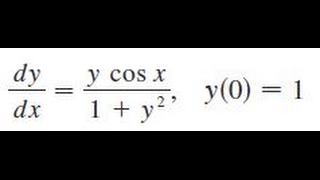



Dy Dx Y Cos X 1 Y 2 Y 0 1 Youtube



Find The General Solution Of Differential Equation X 2 Y 1 Dx Y 2 X 1 Dy 0 Sarthaks Econnect Largest Online Education Community
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve `(xy1)dx (2x 2y3)dy=0`Find dy/dx y= (x^2)/ (3x1) y = x2 3x − 1 y = x 2 3 x 1 Differentiate both sides of the equation d dx (y) = d dx ( x2 3x−1) d d x ( y) = d d x ( x 2 3 x 1) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more stepsWe have, \\left( 1 x \right)\left( 1 y^2 \right) dx \left( 1 y \right)\left( 1 x^2 \right)dy = 0\ \ \Rightarrow \left( 1 x \right)\left( 1 y^2 \right



Solve The Differential Equation 1 Y2 Tan 1 X Dx 2y 1 X2 Dy 0 Studyrankersonline




Solve This 1 Dydx Y Y X X Y X 2 3xy Y2 Dx X2 Xy Dy 0 Maths Differential Equations Meritnation Com
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals int (((xy)/2)^2 (1(xy)/2)^2) dx dy, x=0 to 1, y=0 to 1 Extended Keyboard;Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more The general solution of y^2dx (x^2 – xy y^2)dy = 0 is (A) tan^1(x/y) logy c = 0 asked in Differential equations by Sarita01 ( 535k points) differential equations




Solve Each One Of The Following Differential Chegg Com
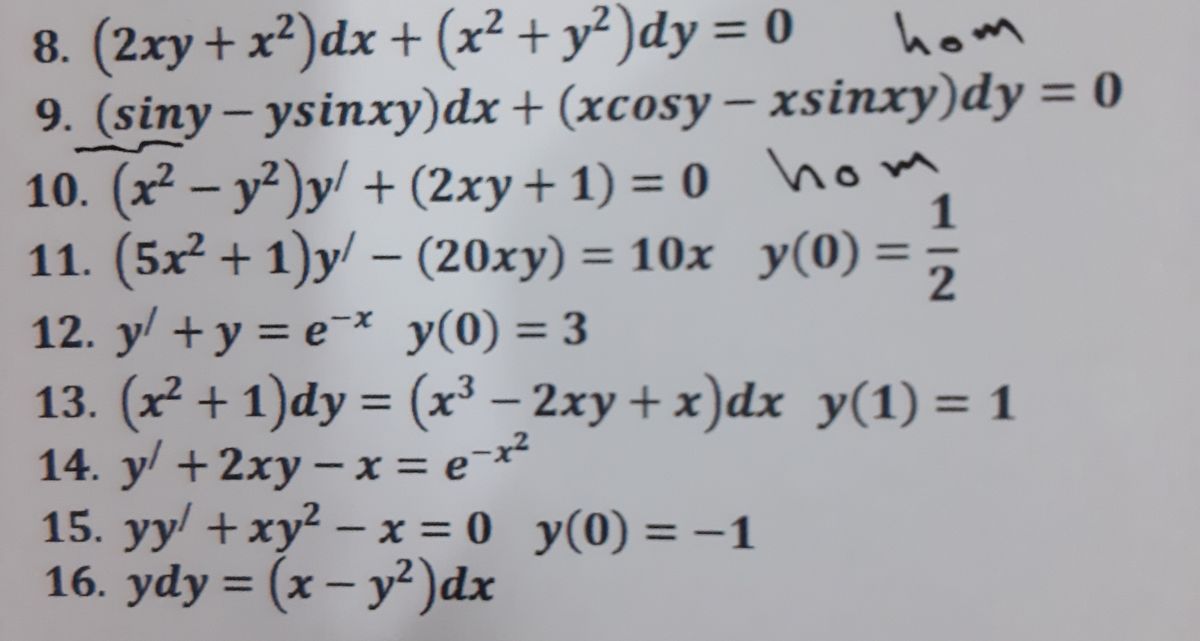



Answered 8 2xy X Dx X Y Dy 0 3d Bartleby
y= sqrt ( 2 sqrt(x^21) ) IF its actually x2ysqrt(x^21)dy/dx = 0 then we can say that 2ysqrt(x^21)dy/dx = x So 2ydy/dx = x/sqrt(x^21) Integrating both sides int \2 ydy/dx \ dx=int \ x/sqrt(x^21) \ dx 2 int \ d/dx(y^2/2) \ dx= int \ x/sqrt(x^21) \ dx = int \ d/dx( sqrt(x^21)) \ dx implies y^2= sqrt(x^21) C y^2= C sqrt(x^21) y= pm sqrt ( C sqrt(x^21Rewrite 2xy dxx2 dy−1 dy = 0 2 x y d x x 2 d y − 1 d y = 0 Change the sides $$2 xy \ dx x^2 \ dy = 1 \ See full answer belowSimple and best practice solution for (xx*y^2)dx(1x^2)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it



Find The General Solution Of Differential Equation X 1 Y 2 Dx Y 1 X 2 Dy 0 Sarthaks Econnect Largest Online Education Community
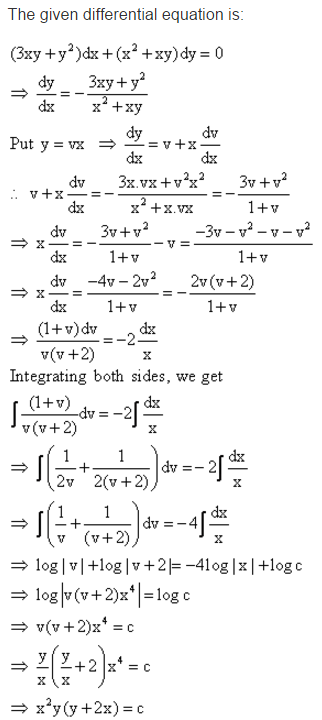



Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Mathematics Topperlearning Com D1ksg633
Ex 96, 11 For each of the differential equation find the general solution 𝑦 𝑑𝑥 𝑥− 𝑦2𝑑𝑦=0 Step 1 Put in form 𝑑𝑦𝑑𝑥 Py = Q or 𝑑𝑥𝑑𝑦 P1 x = Q1, y dx (x − y2) dy = 0 y dx = − (x − y2)dy 𝑑𝑦𝑑𝑥 = −𝑦𝑥− 𝑦2 This is not of the form 𝑑𝑦𝑑𝑥 Py = Q ∴ we findSolve 1/(x y(x) 1)^2 ( dy(x))/( dx) (x^2/(x y(x) 1)^2 y(x)^2) = 0 Let P(x, y) = 1/(x y 1)^2 and Q(x, y) = y^2 x^2/(x y 1)^2 This is an exact1) Solve the given initialvalue problem (x y)2 dx (2xy x2 − 3) dy = 0, y(1) = 1 2) Find the general solution of the given differential equation x dy/dx (4x 1)y = e−4x y(x) = Give the largest interval over which the general solution is defined (Think about the implications of
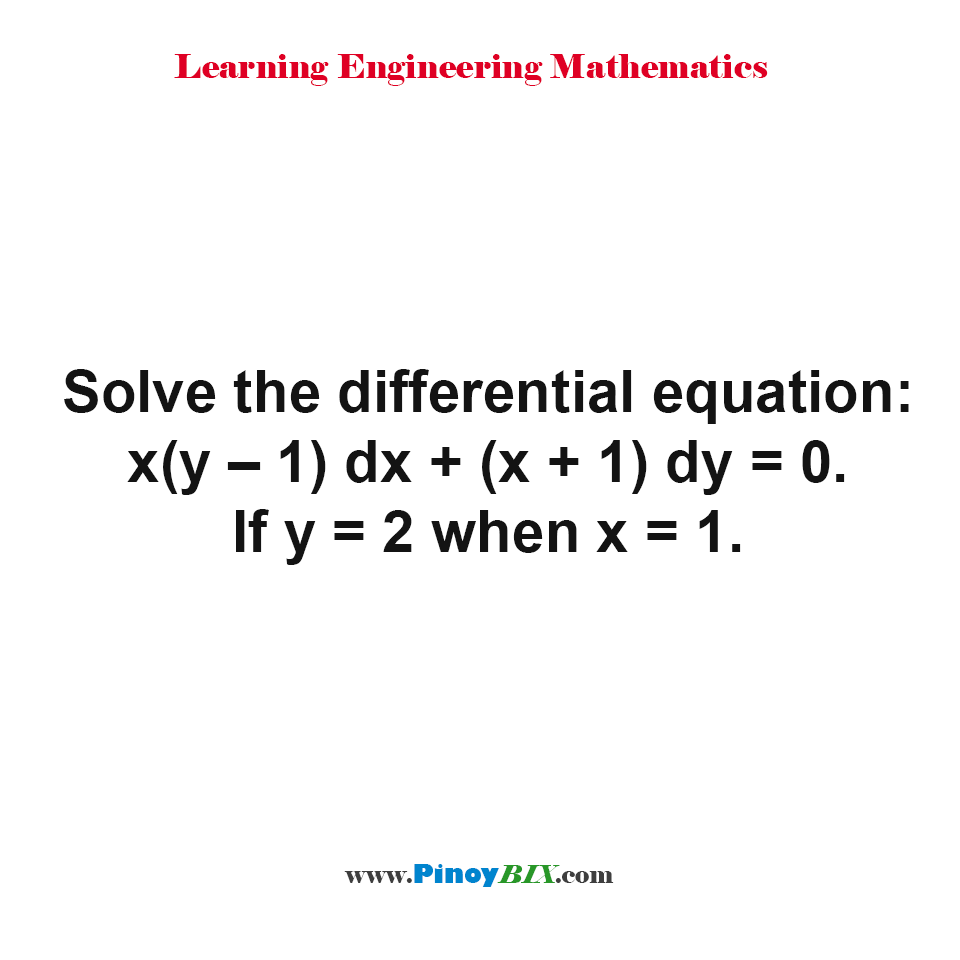



Solution Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If Y 2 When X 1
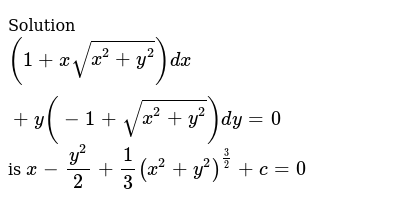



Solution 1 Xsqrt X 2 Y 2 Dx Y 1 Sqrt X 2 Y 2 Dy 0 Is X Y
8 Problem y 2 √ 1−x dy = sin1(x)dx with y(0) = 1 To put into standard form, we'll be dividing so that x 6= ±1 In that case, Z y2 dy = Z sin−1(x) √ 1−x2 dx The right side of the equation is all set up for a u,du substitution, with u = sin−1(x), du = 1/ √ x2 −1dx 1 3 y3 = 1 2 (arcsin(x))2 CX 2 Y 1 Dx Y 2 X 1 Dy 0 いわき 市 考古 Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com For more information and source, see on this link httpsTenemos una ecuación diferencial de la forma M (x, y) dx N (x, y) dy = 0 La ecuación es exacta si ∂M / ∂y = ∂N / ∂x M (x, y) = xy y² y —> ∂M / ∂y = x 2y 1 N (x, y) = x² 3xy 2x – → ∂N / ∂x = 2x 3y 2 La ecuación no es exacta




Solution 1 Xsqrt X 2 Y 2 Dx Y 1 Sqrt X 2 Y 2 Dy 0 Is X Y




4 Solve The Exact Differential Equation 1 2xy Dx 4y3 X2 Dy 0 4 Solve The Exact Differential Equation Homeworklib
Math 334 Assignment 1 — Solutions 6 Solution We look for an integrating factor of the form µ = µ(xy) Multplying through by µ gives µ(xy)M(x,y)dxµ(xy)N(x,y)dy = 0, Answered Solved Solve differential equation dx/dyx/y= 1/(sqrt(1y^2)) The integrating factor method, which was an effective method for solving firstorder differential equations, is not a viable approach for solving seco y(xy1)dxx(1xyx^(2)y^(2))dy=0 Updated On 271 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!




Differential Equations Solved Examples 17



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf
P(x,y)dxQ(x,y)dy = 0 where P(x,y) = 2(y 1)ex Q(x,y) = 2(ex −2y) ∂P ∂y = 2e x = ∂Q ∂x, ∴ ode is exact ∴ u(x,y) exists such that du = ∂u ∂x dx ∂u ∂y dy = P dxQdy = 0, Giving i) ∂u ∂x = 2(y 1)e x, ii) ∂u ∂y = 2(e −2y) Integrate i) u = 2(y 1)ex φ(y) Differentiate ∂u ∂y = 2e x dφ dy = 2(e x



Solved For Each Of The Following Obtain A Particular Solution Satisfying The Initial Condition Indicated 2y Dx 3x Dy When X 2 Y 3 2 Course Hero



Solve Each Differential Equation 1 X Dy Y Dx Chegg Com



Www Tau Ac Il Levant Ode Solution 6 Pdf



How Do You Solve Dy Dx Y 2xsqrt 1 X 2 Where Y 1 When X 0 Socratic



1
.png)



Q15 X X2 3y2 Dx Y Y2 3x2 Dy 0 Y 1 1 Maths Differential Equations Meritnation Com



What Is The Solution Of This Differential Equation Y X 2 Y 2 1 Dx X X 2 Y 2 1 Dy 0 Quora




Math 432 Hw 2 5 Solutions Frostburg




Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation




Solve The Following Differential Equation X Sqrt 1 Y 2 Dx Y Sq



What Is The Solution Of The Differential Equation 1 X 2 Dy 1 Y 2 Dx 0 Quora




First Order Differential Equations Ppt Download




Sqrt 1 X 2 Dy Sqrt 1 Y 2 Dx 0




Math 432 Hw 2 5 Solutions Pdf Free Download




X2 2xy Y2 Dx X Y 2dy 0 Brainly In



Q Tbn And9gcqqdjererih8cbajqv Puntih4ikbw7iy9bdv7cgyhxgixkwubp Usqp Cau




Unit 03 Differential Equations Doc Logical Truth Equations




X Y Dx Dy 0 Novocom Top




How To Solve Math 1 X 2 Dy 1 Y 2 Dx Math Quora




X Y 1 Dx Y X 1 Dy 0find The General Solution Of The Differential Equation Brainly In




Solution Of Y Xy 1 Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange
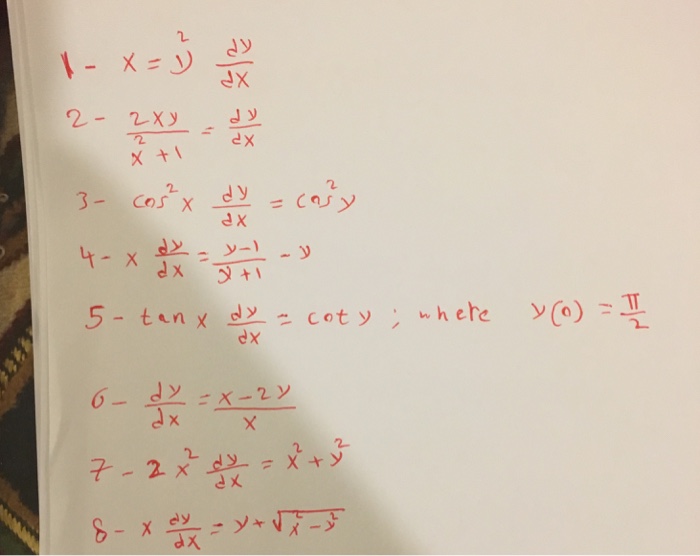



X Y 2 Dy Dx 2xy X 2 1 Dy Dx Cos 2x Dy Dx Chegg Com




X 2 Y 2 Dx 2xy Dy 0 Youtube



How To Solve 1 Y 2 Dx 1 X 2 Dy 0 Quora



3 8 Implicit Differentiation Calculus Volume 1




Solve The Equation E Xsqrt 1 Y 2 Dx Y Xdy 0




Sqrt 1 X 2 D X Sqrt 1 Y
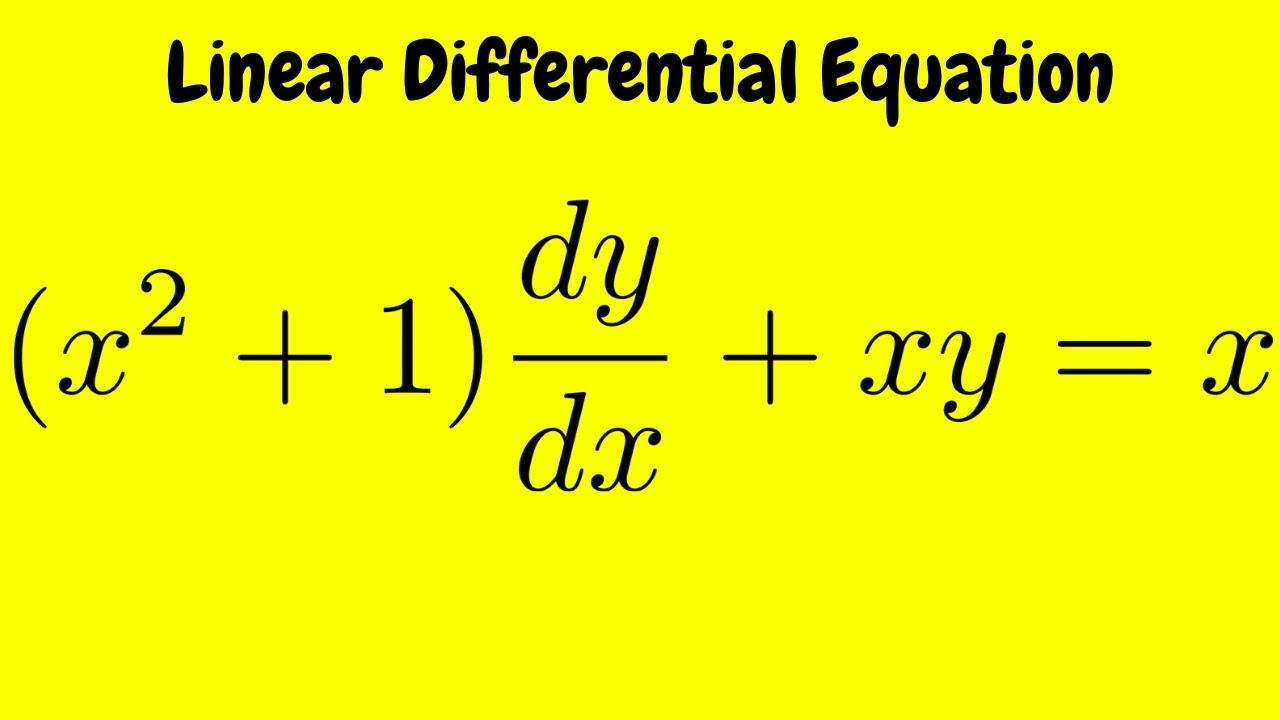



Solve The Linear Differential Equation X 2 1 Dy Dx Xy X Youtube




Ppt First Order Differential Equations Powerpoint Presentation Free Download Id



Www Ualberta Ca Csproat Homework Math 215 Solution 3 Pdf




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection




Solve The Given Differentia By Separation Of Chegg Com
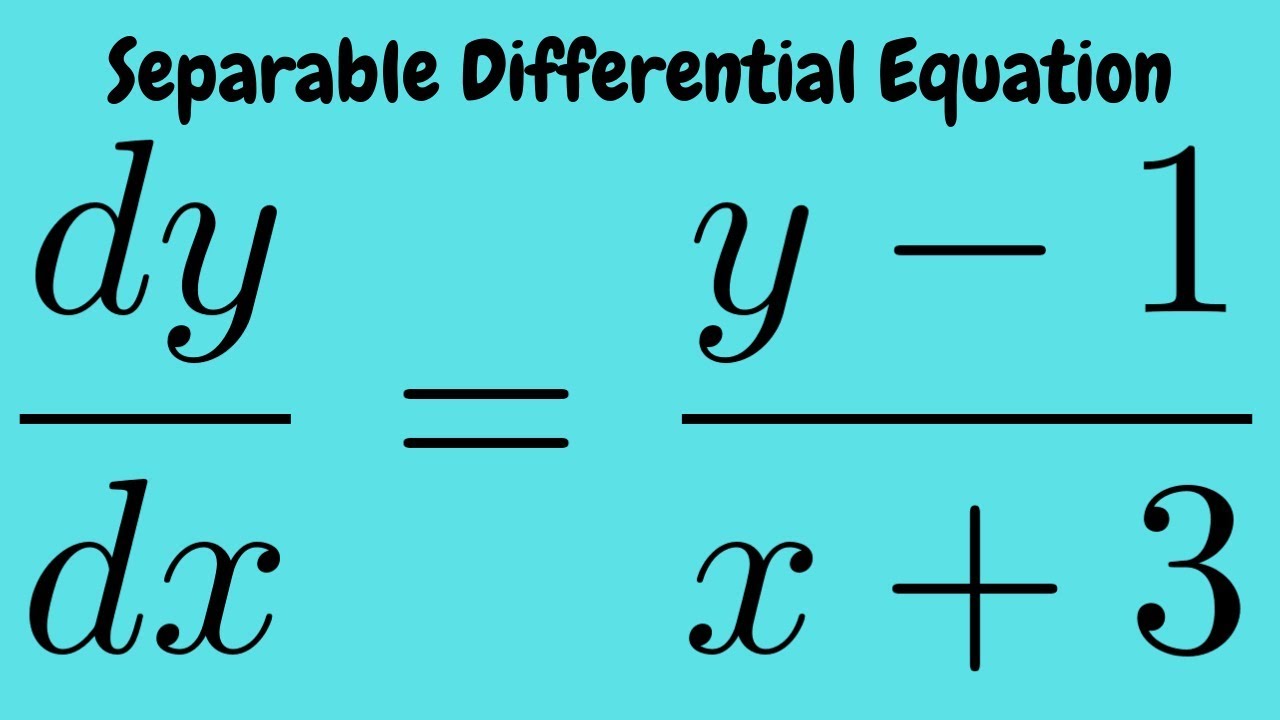



Initial Value Problem Dy Dx Y 1 X 3 With Y 1 0 Separable Differential Equation Youtube




Solve Each Differential Equation 1 X Dy Y 2 Dx Chegg Com




Exact Equations Example 3 Video Khan Academy




Solve The Following Different Al Exercise Begin Array Ll Text I Y 2 D X Left X Y X 2 Right D Y 0 Text Exercise Text Ii X 2 Y D X Left X 3 Y 3 Right D Y 0




Example 10 Find General Solution Dy Dx 1 Y2 1 X2 Examples



Solved Solve The Following Differential Equations X Y 3 Dx X Y 1 Dy 0 2 X Y 1 Dx 3x 4y 2 Dy C 3 1 Y 2 Xy 2 Dx X 2y Y 2xy Dy Course Hero




Slides Show




Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy




Solve Each Differential Equation X Dy Y 2 Dx 0 Chegg Com



Http Fractal Math Unr Edu Ejolson 285 15 Extraprob Pdf




Y X 2 Dx Dy 0 Novocom Top




Solve The Following Differential Equation 1 1 3 Y X Dy Dx Y 3 X 1 2 Ln X Y X Dx Ln X Dy 3 X 2 Y 2 Y 4sin X Dx 2xy 4y 3cos X Dy 4 Tan X 8sin X Sin Y Dx 8cos X Cos Y Dy 0 5 1 Y 2sin 2x Dx Ycos 2x Dy 0 Wegglab



Solve The Differential Equation 1 Y 2 Tan 1x Dx 2y 1 X 2 Dy 0 Sarthaks Econnect Largest Online Education Community




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download




Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection



Consider The Differential Equation Y 2dx X 1 Y Dy 0 If Y 1 1 Then X Is Given By Sarthaks Econnect Largest Online Education Community
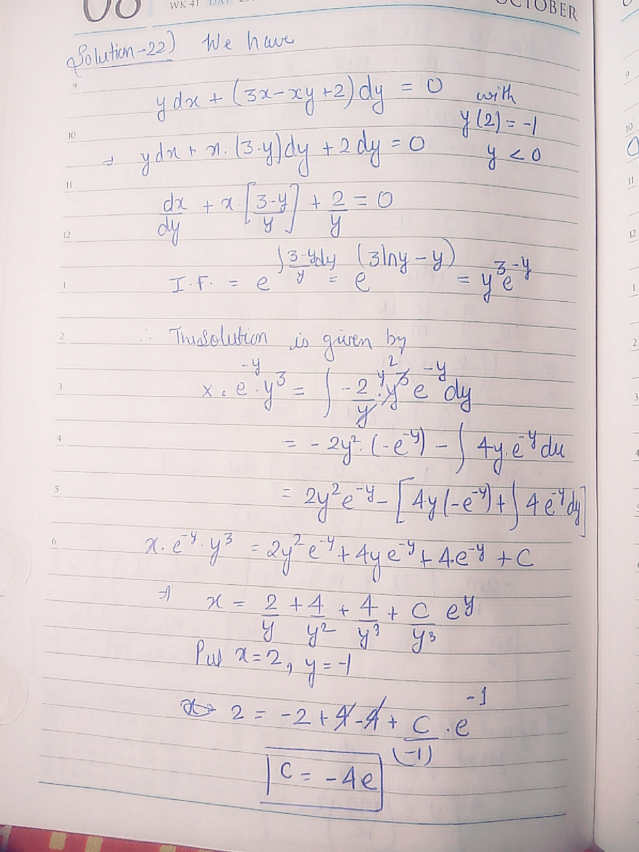



Solve The Initial Value Problem Y Dx 3x Xy 2 Dy 0 Y 2 1 Y 0 Homework Help And Answers Slader




Solve The Differential Equation X 1 Y 2 Dx Y 1 X 2 Dy




Solution 1 Xsqrt X 2 Y 2 Dx Y 1 Sqrt X 2 Y 2 Dy 0 Is X Y




Solve X 2 Yx 2 Dy Y 2 Xy 2 Dx 0




Answered 2 Dx Y 0 Dt D X D Y X Y Bartleby




Math 432 Hw 2 5 Solutions



Solve 2 Y 3 Xy Dy Dx 0 Given That Y 1 2 Studyrankersonline




X 1 Y2 Dx Y 1 X2 Dy 0 Brainly In




Engineering Mathematics Notes




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When




Differential Equations Solved Examples Solve The Ivp 2xy X 4 Dx X 2 Y 2 Dy 0 Y 0 1



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf




Misc 6 Find General Solution Dy Dx Root 1 Y2 1 X2 0
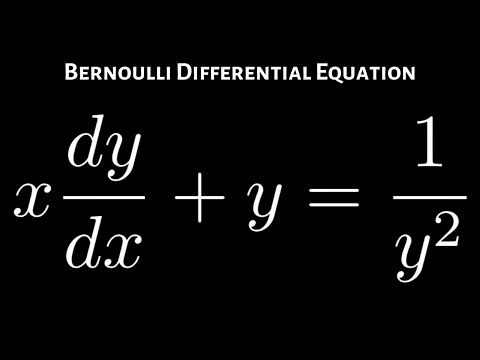



Homogeneous Differential Equation Y 2 Yx Dx X 2dy 0 Topic Play




Ma 104 Differential Equations




Ordinary Differential Equations




X 1 Y 2 Dx Y 1 X 2 Dy 0 Youtube




Solve The Initial Value Problems A X 2 Dy Dx 4x 2 Chegg Com




Solve 3xy 2ay 2 Dx X 2 2axy Dy 0 Mathematics Stack Exchange




Y 1 X 2 Y X 1 Y 2 0 Novocom Top




Math X 2dx Y X 1 Dy 0 Math Homework Help And Answers Slader




Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com
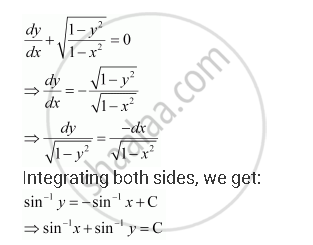



Find The General Solution Of The Differential Equation Dy Dx Sqrt 1 Y 2 1 X 2 0 Mathematics Shaalaa Com




What Is The Solution For Math Sqrt 1 X 2 Sqrt 1 Y 2 Dx Xy Dy 0 Math Quora




Need Help On 8 9 And 10 Please 1 Point Use Substitution To Find The General Solution Homeworklib



Solved 3x 8 Y 2 4 Dx 4y X 2 5x 6 Course Hero



1


