Equation is linear if dependent variable y is not being multiplied by variable x sin (y) and cos (y) make equation non linear Now i went to a site and they said following equation is linear x^2y'' xy' (x^2v^2)y = 0 y'' is being multiplied by x^2 and also y' being multiplied by x2) The digital system in y ( n ) = x ( n 2 ) is a) nonlinear and causal b) linear and causal c) linear and noncausal d) nonlinear and noncausal 3) The system described by y n = nx n is a) Linear, time varying and stable b) Nonlinear, time invariant and unstable c) Nonlinear, time varying and stable The input signal x (t) is varied at fixed value of t (let 1 sec) Then see how the output y (t) is varying at the same value of t If the relationship between y and x is linear (straight line) and crossing through origin then the system is linear If you find any time t at which the system is not linear then the system is nonlinear
Jstor Org
Y(n)=x^2(n) linear or nonlinear
Y(n)=x^2(n) linear or nonlinear-4 Nonlinear systems Maxim Raginsky Lecture III Systems and their properties What is a system?For example, for real numbers, the map x x → x 1 is non linear So is the mapping x → x 2, also over real numbers The following series of three images illustrates the linear function f R 2 → R 2 with f(x, y) = (2x, y) The y component of the vector remains the same, while the x component is scaled by two, as shown in the first image




Pdf Existence Of Positive Solutions For A Third Order Multi Point Boundary Value Problem
Math 341 Worksheet 1 Fall 10 2 Solutions of ODEs DEFINITION solution Any function φ, defined on an interval I and possessing at least n derivatives that are con tinuous on I, which when substituted into an nth order ODE reduces the equation to an identity, is said to be a solution of the equation on the interval(An interval is a continuous Nonlinear System Any system is called nonlinear that does not satisfy two properties (i) Additivity (ii) Homogeneity Example Determine whether or not each of the following systems are linear with input and output (i) (ii) Solution (i) AdditivityQuestion is ⇒ The discrete time system describes by y ( n ) = x ( n 2 ) is, Options are ⇒ (A) casual, Linear, time varying, (B) casual, nonlinear, timevari, noncasual, Linear, time invariant, (D) noncasual, nonlinear, time variant, (E) , Leave your comments or Download question paper
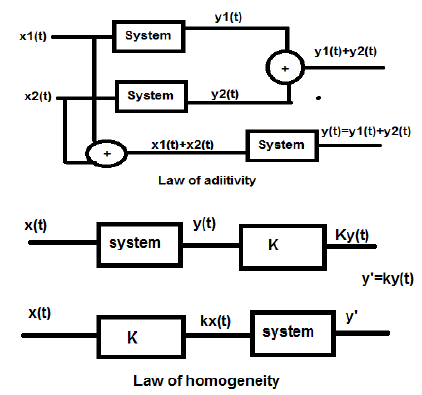
Example yn = xn2 is not linear since (2yn) = (2xn)2 does not reduce to yn = xn2 Of course, here it is easy to see that doubling the input quadruples the output Example yn−2yn−1nyn−2= 3xn4xn−1 is linear since doubling it yields 2yn−4yn−1(a) yn = xn xn 11 = Txn The system is linear because Tax1n bx2 n = ax1n ax1n 1 bx 2n bx2n 1 = aTx1 n bTx 2n 1 The system is timeinvariant because yn = xn xn 1 = Tjxn, Txn N = xn N xn 1 N = yn NConcept Linearity Necessary and sufficient condition to prove the linearity of the system is that the linear system follows the laws of superposition ie the response of the system is the sum of the responses obtained from each input considered separately y{ax 1 t bx 2 t} = a y{x 1 t} b y{x 2 t} Conditions to check whether the system is linear or not
Iy(n) = A x(n) Iy(n) = n x(n) Iy(n) = p x(n) x2(n 2) Iy(n) = x( n) Iy(n) = x(n 1) Iy(n) = 1 1 x(n2) Iy(n) = e3x(n) Ans Y, N, Y, N, Y, Y, Y Dr Deepa Kundur (University of Toronto)DiscreteTime Signals and Systems15 / 36 Chapter 2 DiscreteTime Signals and Systems Linear vs Nonlinear Systems ILinear system obeys superposition principle (b)Sketch the output signal, y(n), produced by the 4point input signal, x(n) illustrated below 2 3 2 12 1 0 1 2 3 4 5 6 n x(n) (c)Classify the system asThere should not be any nonlinear operator present in the system Causality A system is causal, if the output of the system does not depend on future inputs, but only on past input




Linear Nonlinear Functions Table Video Khan Academy




Solved Problem 1 For Each Of The Below Systems With Input X Chegg Com
Free linear equation calculator solve linear equations stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy24 c JFessler,May27,04,1310(studentversion) 212 Classication of discretetime signals The energy of a discretetime signal is dened as Ex 4= X1 n=1 jxnj2 The average power of a signal is dened as Px 4= lim N!1 1 2N 1 XN n= N jxnj2 If E is nite (E < 1) then xn is called an energy signal and P = 0 If E is innite, then P can be either nite or innite3 1 4 15) A system is said to be linear if it satisfies Homogeneity



Time Variant And Time Invariant System



Jntuhsd In
It forms a curve and if we increase the value of the degree, the curvature of the graph increases The general representation of linear equation is;² x(t) y(n)=x(2n) y(n)=x(n)x(n2) Now if the system is actually LTI, then its output should satisfy y 2 n = y 1 n − 1 However one can see that this is not the case, as y 2 n = δ n − 1 ≠ y 1 n − 1 = 0 Hence this counterexample has proved that the claim was wrong;



Scielo Conicyt Cl




Solved 1 Determine Whether Each Of The Following Systems Chegg Com
Y 3 (n)=y 1 (n)y 2 (n)= x 1 2 (n) x 2 2 (n)≠(x 1 (n)x 2 (n)) 2 So the system is nonlinear QUESTION 9 If the output of the system of the system at any 'n' depends only the present or the past values of the inputs then the system is said to be AY = x2 y = x 2 A linear equation is an equation of a straight line, which means that the degree of a linear equation must be 0 0 or 1 1 for each of its variables In this case, the degree of variable y y is 1 1 and the degree of variable x x is 2 2 Not Linear Homework Statement For each of the following systems, determine whether or not the system is TimeInvariant, Linear, and causal a) yn = xncos(02*pi*n) there are more but if I can figure this out I should be able to get the others Homework Equations Time Invariant




Answered 4 A Characterize The Following Bartleby
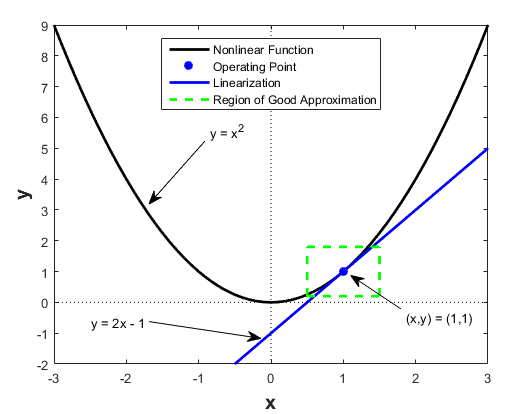



Linearize Nonlinear Models Matlab Simulink
Ie, the system is not LTI In fact, what we have actually shown is that the system isThe given discretetime system is y n = x n 2 is linear since there is no constant term as well as square terms in input and output noncausal since for any value of n except 0 and 1, output depends upon the future value of the input for example at n = –For each of the systems below, determine whether or not the system is (1) linear, (2) timeinvariant, and (3) n y 2n = x 2n wn= ay 1n by 2n = a x 1n bx 2n xn= ax 1n (S29) are not equal, system (f) is nonlinear Solution Timein variance F or each dif ference equation abo ve, we compute and in Figure 2 below;



Solved Electrical Engineering Tutors This Is Urgent Answer Along With Matlab Required Within 2 Hours Course Hero




Nonlinear Systems Springerlink
Y n x n( ) ( )2 is a) Causal, linear and time varying b) Causal, non linear and time varying c) Non Causal, linear and time varying d) Non Causal, Non linear and time varying Ans c) 4 Find the range of a for which the LTI system with impulse response h n a u n( ) ( ) n is stable a) a 1 b) a !1 c) a ! A linear function is given in the form where and are both constant Function 1 72 = x³ y ⇒ rearranging to make 'y' the subject we have y = x³ 72 This function has 'x³' not 'x', so this function is nonlinearFunction 2 y 1 = 5(x 9) ⇒ Multiplying out and simplify like terms y 1 = 5x 45 y = 5x 45 1 y = 5x 46The order to solve such type of problems, check causality, linearity and time invariant one by one The given system y (n) = x (n 2) is noncausal Because for any negative value of n the output goes to future For example




Pdf Existence Of Positive Solutions For A Third Order Multi Point Boundary Value Problem




Describing Function Analysis Of Nonlinear Systems Electrical4u
Answer (1 of 2) It is linear because y(t) is linear function of x() Irrespective of x may be function of linear or nonlinear function of t (it doesn't matter sint or t^2 or 2*t)so it is linear system although if this function is modified to y(t)=sinx(t) then it would be non linear function3 Moving average (MA) filter yn = xn−1xnxn1 3 — not causal, since the output at time n depends in part on the input at = at2x(t) = aS n x(t) o The system is linear Maxim Raginsky Lecture III Systems and their propertiesA general optimization problem is to select n decision variables x1,x2,,xn from a given feasible region in such a way as to optimize (minimize or maximize) a given objective function to give a nonlinear extension to any linear program Moreover, the constraint x =0 or 1 can be modeled as x(1 −x) =0 and the constraint x integer as sin




Gate Ese Linear And Nonlinear Systems Numericals Offered By Unacademy




Discrete Time Signal An Overview Sciencedirect Topics
Transcribed Image Textfrom this Question (1) Static or dynamic (2) Linear or nonlinear (3) Time invariant or time varying (4) Causal 01 noncausal (5) Stable or unstable Examine the following systems with respect to the properties above (a) y (n)cos x (n) (b) y (n) = x (k) (c) y (n) = x (n)cos (w0n) (d) y (n) = x (n 2) (e) ?n) = Trun x (nIf n → ∞, input signal always remains finite and input remains finite too The given system remains finite, ∴ System is stable//googl/JQ8NysSolve the Nonlinear System of Equations x^2 y^2 = 4, 7x^2 7y^2 = 2




Linear And Non Linear Systems Solved Problems Part 1 Youtube




Digital Signals And Systems Ppt Video Online Download
(a) y(n) = cos(x (n) (b) y(n) ^ (c) y (n) ==x (n) cos(mon) Question A discretetime system can be (1) Static or dynamic (2) Linear or nonlinear (3) Time invariant or time varying (4) Causal or noncausal (5) Stable or unstable Examine the following systems with respect to the properties above (a) y(n) = cos(x (n) (b) y(n) ^ (c) y (nN n dx dy d y F x y Differential equations are classified into linear DEs or nonlinear DEs An nth order differential equation is said to be linear if it can be written in the form that is, it satisfies the following two conditions (1) the dependent variable (y) and all itsNow, in order for this to be a linear equation, the ratio between our change in y and our change in x has to be constant So our change in y over change in x for any two points in this equation or any two points in the table has to be the same constant When x changed by 4, y changed by negative 1 Or when y changed by negative 1, x changed by 4



Math Uaic Ro




Nonlinear Transformation An Overview Sciencedirect Topics
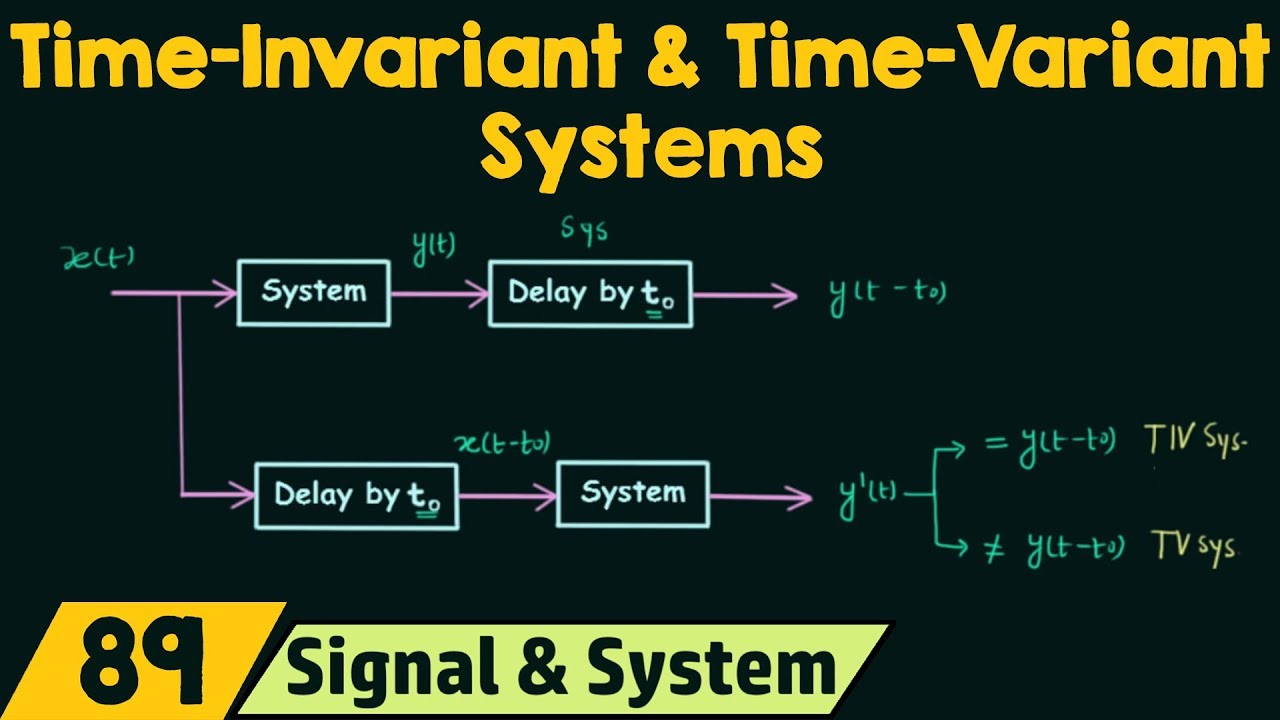
Therefore, system is NonLinear Time Variant or Time Invariant;Y{ax 1 n bx 2 t} = a y{x 1 n} b y{x 2 n} Conditions to check whether the system is linear or not The output should be zero for zero input;Nonlinearsystemofequationscalculator 3x^2=y, x1=y en Related Symbolab blog posts High School Math Solutions – Systems of Equations Calculator, Nonlinear In a previous post, we learned about how to solve a system of linear equations In this post, we will learn how



Utdallas Edu




Nonlinear Mapping An Overview Sciencedirect Topics
The function is non linear EXPLANATION A linear function is of the form or The highest degree of the variables in each term in the simplest form is 1 Any degree higher or less than 1 will make the function nonlinear The function given to us is, The highest degree is 2 This is a quadratic curve The graph of all linear functions are straightIt is linear because y(t) is linear function of x() Irrespective of x may be function of linear or nonlinear function of t (it doesn't matter sint or t^2 or 2*t)so it is linear system although if this function is modified to y(t)=sinx(t) then it would be non linear function because now y is a non linear function of xY = mx c Where x and y are the variables, m is the slope of the line and c is a constant value The general representation of nonlinear equations is;




How To Convert Non Linear Equations To Linear Form Y Mx C Youtube



Y N Cos X N Is Linear Or Non Linear Quora
Linear DiscreteTime System • For the causal accumulator to be linear the condition must hold for all initial conditions , , , and all constants αand β • This condition cannot be satisfied unless the • Hence, the median filter is a nonlinear discretetime system {y 1ny 2n}={3, 3, 3} btw, your function I'm assuming really should be yn = xn ^ 2 so to test for linearity you would do something like y1 = 1^2 = 1, y2 = 2^2 = 4, y1 2 =9, but 9 != 41 so it is non linear, proof by counter example2 y(t)=x (t) y(n)=x(n) y(n)=2x2(n) A System is said to be dynamic or memory system if the response depends upon past or future inputs For example, the systems defined below are dynamic or memory systems y(t)=x(t1) y(t)=x(t)x(t2) y(t)= ²𝑥 ;



R Nonlinear Regression Analysis All Inclusive Tutorial For Newbies Dataflair




1 Digital Signal Processing Lecture 3 4 By Dileep Kumar Ppt Download
Using the definition of linear system as one which can be put in the form y 0 a 1 y 1 ⋯ a n y n = b 0 x 0 ⋯ b m x m because of the multiplicative term y ( n) y ( 2 n) we can conclude that the system is nonlinear ShareFig 8 Block Diagram of Linear and NonLinear Systems So, iff y'(n) = y''(n) then the system is said to be linear I the system does not fulfills this property then the system is a nonLinear system For example, y(n) = x (n 2) { linear } y(n) = Ax(n) B {non – linear } y(n) = nx(n) { linear }Nonlinear None of these 13) A system is defined by the inputoutput relationship Y(n)= 2x(n) 1/x(n1) The system is Linear Nonlinear None of these 14) From causal/noncausal experiment, for system 2 what will be the delay for which the system will be causal ?




Pdf Nonlinear Decoupling Control Of A Synchronous Motor




Solved For Each Of The Following Systems Determine Whether Chegg Com
View Assignment_1_Solutionpdf from ECE 351 at California State University, Northridge Linear vs NonLinear Systems 1 y(n) = x(n) 1 → 1 = 1 2 → 2 = 2 {1 2 ()} → 1Please Subscribe here, thank you!!!Y(n, k) = ax(nk) 2 bx(nk) y(nk) = ax(nk) 2 bx(nk) y(n, k) = y(nk) Therefore, System is Time Invariant Stable or Unstable;
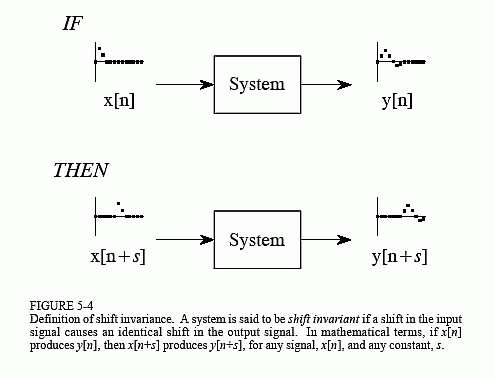



Requirements For Linearity



Bharathuniv Ac In
A system possessing no memory has its output depending upon the input at the same time instant, which is prevalent only in option b QUESTION 19 State if the following system is periodic or not y (t) = sin (√ (2)*x (t)) A No B Yes Solution The function y = sin (nx) is periodic only for rational 'n'1 fx() 1= is a polynomial of degree 0 2 14 23 Hx x=− is a polynomial of degree 1 3 2 3 3 11 R xx x=− is a polynomial of degree 2 4 72 4 3 3 3 Fx x x x=− − is a polynomial of degree 7 The graphs of polynomial functions can sometimes be very complicated For example the graph of 74 2 1




Solved Determine Whether The Following Systems Are Linear Chegg Com




Solved Determine Whether The System Is 1 Stable 2 Causal Chegg Com



1



Dspillustrations Com



Web Mit Edu




Solved Examine The Following Systems With Respect To The Chegg Com



Bharathuniv Ac In



Jstor Org



1




Solved For Each Of The Following Systems Determine Whether Chegg Com




Solved Problem 2 State With A Brief Explanation If The Chegg Com




Bme 452 Biomedical Signal Processing Lecture 2 V




Recognizing Linear Functions Video Khan Academy




Solved Questions Set 3 Ct And Dt Systems Properties Consider The Ct System Represented By The Following Output Y T X T Cos Wot 6 Marks 3 Marks Determine Whether This System Is Justify



Exercises In Signals Systems And Transforms Pdf Free Download




Solved A Discrete Time System Can Be 1 Static Or Dynamic Chegg Com




Ordinary Differential Equation Wikipedia




Solved 1 Determine Whether Each Of The Following Systems Chegg Com




Identifying Linear Nonlinear Functions Using Graphs Tables Video Lesson Transcript Study Com




Is Y T X T A Linear Or A Nonlinear System Quora




Solved Q1 X N And Y N Are The Input And Output Signals Of Chegg Com
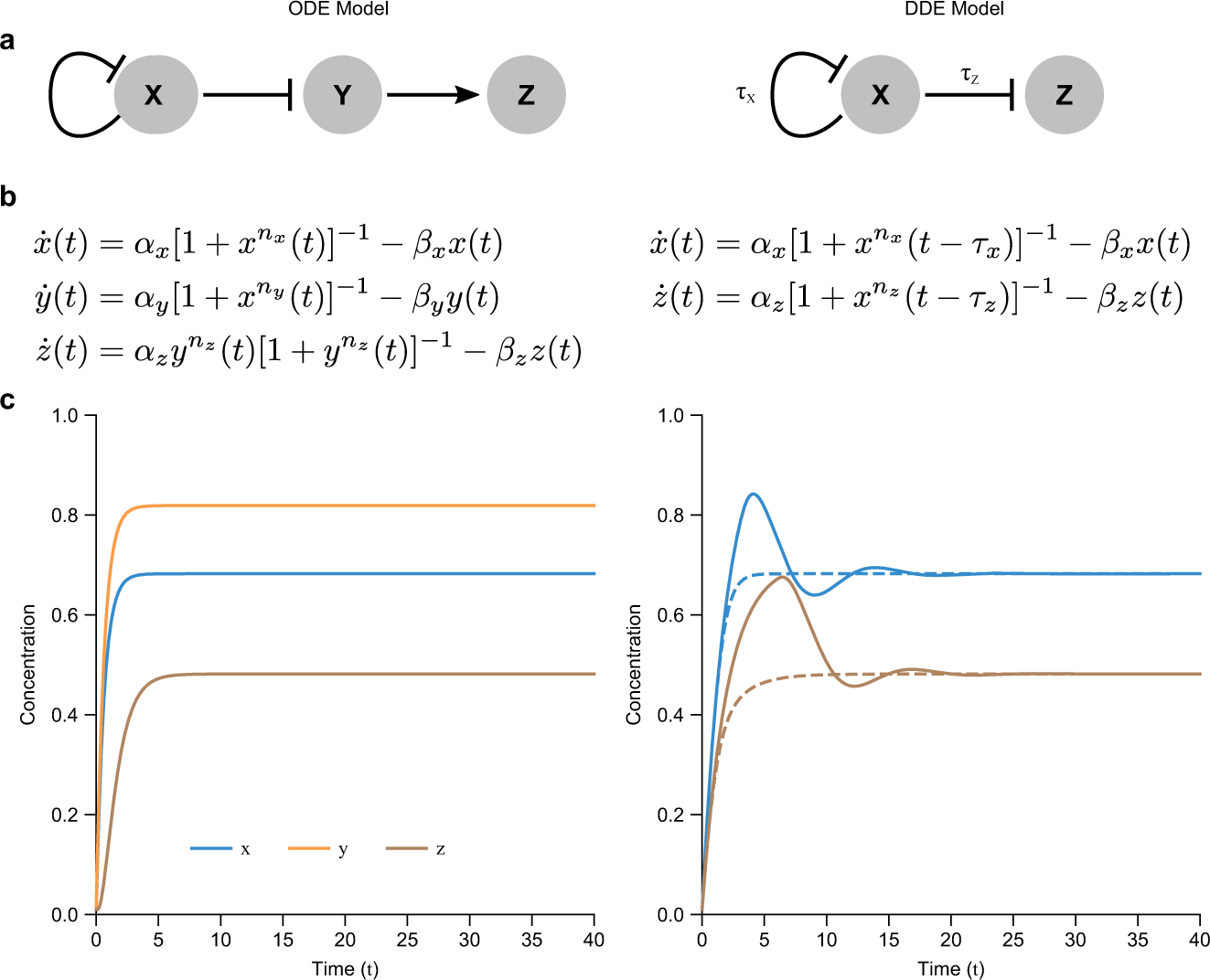



Nonlinear Delay Differential Equations And Their Application To Modeling Biological Network Motifs Nature Communications




Eee 301 Signal Processing And Linear Systems Dr Ppt Video Online Download



Web Mit Edu



Digital Signal Processing Linear Systems




Solved Determine Which Of The Following Systems Is Linear Chegg Com




Demonstrate Step By Step If The Following System Is 1 Static Or Dynamic 2 Linear Or Homeworklib




3 Signals And Systems Part Ii Pdf Free Download




Solved A Discrete Time System Can Be 1 Static Or Dynamic Chegg Com




1 Signals And Systems Fall 03 Lecture 2 9 September Some Examples Of Systems 2 System Properties And Examples A Causality B Linearity C Ppt Download




Pdf Oscillatory Behavior Of A Class Of Nonlinear System Of First Order Difference Equations



Sciencedirect Com



Solved Examine The Following Systems With Respect To The Properties Static Dynamic Linear Nonlinear Time Variant Time Invariant Causal Noncausa Course Hero




Linear Filter An Overview Sciencedirect Topics
:max_bytes(150000):strip_icc()/LinearRelationshipDefinition2-a62b18ef1633418da1127aa7608b87a2.png)



Linear Relationship Definition




Chebyshev Polynomials Wikipedia




Answered The System Given By The Following Bartleby




Linear Time Invariant System Wikipedia




Systems And Properties Ppt Download




Solved Outcome Co1 1 1 Check Whether The Following Systems Chegg Com




Consider The Nonlinear System X Ln Y 2 X And Y X Y 1 A Find All The Critical Points Homeworklib




Recognizing Linear Functions Video Khan Academy




Ba 275 Quantitative Business Methods Agenda N Simple



Is Muni Cz




Answered A Discrete Time System Can Be 1 Bartleby




How To Recognize Linear Functions Vs Non Linear Functions Video Lesson Transcript Study Com




Addressing Nonlinearities In Monte Carlo Scientific Reports




Test On A Nlse Semi Implicit Method On 1 1 X2 With A Polynomial And Cosine Exact Solution




Answered Let A Nonlinear System Be Represented Bartleby



Dspillustrations Com



Order And Linearity Of Differential Equations




Signals Systems Time Variant Time Invariant Youtube




Support Vector Machines Perceptron Revisited N Linear W



Solved Check Whether The Following Systems Are Static Or Dynamic 2 Linear Or Non Linear 3 Causal Or Non Causal And 4 Course Hero



Link Springer Com




Solved Problem 4 1 Points For Each Of The Following Chegg Com




Dsp 1 1150 Homing Pigeon 1790 Semaphore 19




Solved Question 1 Examine The Following Lti System Yn Chegg Com



Bharathuniv Ac In




Solved For Each Of The Following Systems Prove Chegg Com



Search Q Linear System Examples Tbm Isch



Ualberta Ca




Solution Of Differential Equations With Applications To Engineering Problems Intechopen




Solved I Static Or Dynamic 2 Linear Or Nonlinear 3 Time Chegg Com




Solved Problem 0 80 Points Determine Each Of The Following Chegg Com




Dsp U Lec04 Discrete Time Signals Systems




Discrete Time Signals And Systems Ppt Video Online Download



Time Invariant And Time Variant Systems Youtube




Charpit Method Non Linear Pde Mathematics Stack Exchange




Solved A Determine Whether The Following Systems Are Linear Chegg Com




Solved 2 7 A Discrete Time System Can Be 2 Linear Or Chegg Com




Linear And Non Linear Systems Youtube




Linear And Nonlinear Functions Ppt Video Online Download




Data Mining Concepts And Techniques Chapter 3 Cont



Uio No



Diva Portal Org


